鉴于大家对Excel教程十分关注,我们编辑小组在此为大家搜集整理了“用Office Excel解决经典“鸡兔问题”的五种方法”一文,供大家参考学习
“鸡兔问题”是一道古典数学问题,源自我国古代四、五世纪的数学著作《孙子算经》。算经卷下第三十一题为:“今有雉、兔同笼,上有三十五头,下有九十四足。问雉、兔各几何?”原著的解法为:“上署头,下置足。半其足,以头除足,以足除头,即得。”具体解法即:分别列出总头数(35)和总足数(94),总足数除以二,再减去总头数(94÷2-35),得到兔数为12,总头数减去兔数35-12得到鸡数为23。鸡兔问题本身并不难,使用2元1次方程组的消元算法,可以很快得到答案。我们可以尝试着利用Excel提供的各种计算工具来进行计算,不仅别有趣味,而且还会加深对Excel功能的综合掌握,对于讲授Excel的教师而言,则是典型的一题多解的素材。
一、 利用IF函数试探求解
如图1,创建一个二维表,假设鸡数B2为要求解的单元格,将鸡兔的总头数和脚数分别写入D2和D3单元格,利用已知条件在其他单元格中写入公式:因兔头数=总头数-鸡头数,故在C2单元格中写入=D2-B2;鸡脚数=鸡头数*2,故B3单元格写入=B2*2;兔脚数=兔头数*4,故C3单元格写入=C2*4。
接下来我们在任意其他单元格输入一个判断公式(本例中使用F1单元格),公式内容为=IF(D3=B3+C3,"正解!",IF(D3>B3+C3,"高了","低了"))。公式的本质是判断鸡脚数+兔脚数与总脚数之间的关系,如果判断表达式D3=B3+C3结果为True,就意味着我们已经得到了正确答案。
最后在B2中输入35以内的任意整数进行试探求解。如果输入的数值高于正解,判断单元格F1会提示“高了”,若数值小于正解则提示“低了”,用户根据提示再继续输入其他一个数字,直到输入了正确答案23,F1单元格会显示“正解!”。
这种方法比较直观,但是非常笨拙,需要人工干预。即使用户聪明地使用二分法试探,也需要多次输入才能解决问题,对于更庞大的问题,这种解法几乎是不可行的。
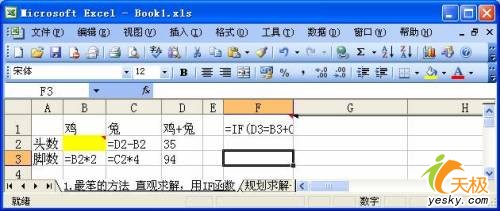
图1 利用IF函数试验求解
二、使用模拟运算表,让Excel自动给出答案
第一种方法存在的问题就是非常繁琐,需要用户干预。为了避免用户干预,可以考虑将鸡兔问题转化为双变量模拟运算表,将鸡数和兔数设置为两个变量。具体做法是:
1. 先在A1:D2单元格中输入参考数据如下(图 2):

图2 参考数据
2. 创建一个二维模拟运算表的框架,因为鸡的数目不会超过脚数/2,即鸡最多为47只,同理兔子数目不会超过94/4,即兔最多为24只。我们用第4行表示兔的数目,用第C列表示鸡的数目。在D4:AA4中填充1,2,3…24等数值,在C5:C47中填充1,2,3…47,参见图 4;
3. 在模拟运算表的左上方C4单元格中输入模拟运算表的公式:=IF(2*A2+4*B2=$C$2,IF(A2+B2=$D$2,"正解","X"),"X"),公式中的$C$2和$D$2单元格为已知的总脚数和总头数,A2和B2将作为模拟运算表的两个变量;
4. 选中模拟运算表区域,即C4:AA47区域,然后选择“数据”菜单中的“模拟运算表”菜单项,打开模拟运算表对话框(如图 3)。在对话框中,输入引用行的单元格为$A$2(即鸡数),输入引用列的单元格为$B$2(即兔数),单击“确定”按钮;
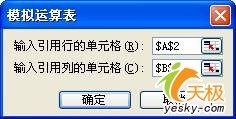
图 3 输入引用行和引用列的单元格
5. 在模拟运算表中会显示出计算结果,在所有的运算表区域中,只有Z16单元格中显示了“正确”两字,其余单元格均为“X”,表示Z16单元格为问题的正解,查表可知,Z16单元格的兔数为12,鸡数为23(如图 4)。
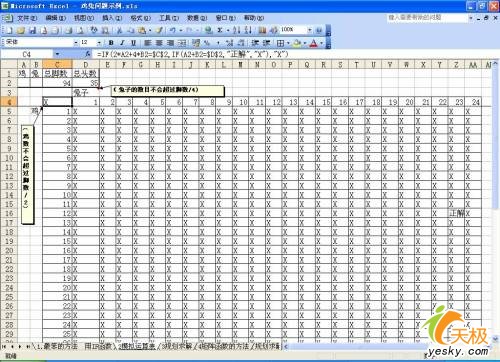
图 4 模拟运算表运算结果
这种使用模拟运算表的方法比较“另类”。利用这种思路,不仅可以求解多元一次方程组,还可以求解多解问题。
三、使用规划求解,将苦活抛给Excel
利用Excel的规划求解功能,我们可以利用计算机高速计算的特性求解鸡兔问题。如果用户的“工具”菜单中没有“规划求解”菜单项,可以选择“工具”à“加载宏”,在“加载宏”对话框中选中“规划求解”并按下“确定”(如图 5