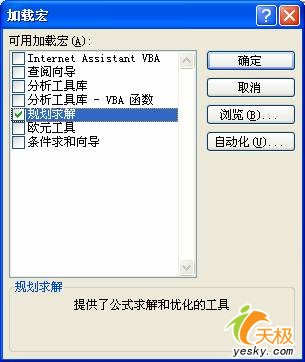
图 5 规划求解加载宏
新建一个工作表,单元格B1为总脚数,输入公式=2*B3+4*B4;B2为总头数,输入公式=2*B3+4*B4,B3和B4单元格用于显示计算鸡数和兔数的结果,暂时留空。为求直观友好,可分别在A1、A2、A3、A4单元格中输入文字提示:“总脚数”、“总头数”、“鸡数”和“兔数”。如图 6所示。
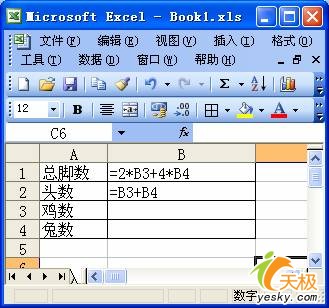
图 6 规划求解表
然后选择“工具”菜单下的“规划求解”,在“规划求解参数”对话框中,设置目标单元格$B$1等于固定值94(即总脚数等于94),将可变单元格设置为$B$3:$B$4,即欲求解的鸡数B3和兔数B4。在“约束”栏中,添加三个约束条件:$B$2=35(即总头数等于35),$B$3和$B$4为整数,如图 7所示。
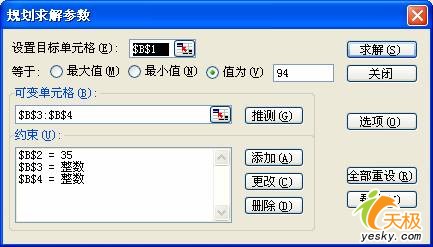
图 7规划求解对话框
规划求解参数设置完毕后,按下“求解”按钮,Excel很快地给出了正确答案:鸡数B3单元格为35,兔数B4单元格为11.99999975。求解结果中兔数为小数形式,是规划求解过程中的计算误差。因为本问题是二元一次方程组求解,属于线性问题,用户可以在规划求解参数对话框中按下“选项”按钮,选中“采用线性模型”即可在计算结果中正确显示整数。
使用规划求解,可以利用计算机高速计算的特点对复杂问题建模求解,同样的思路也适合于解决多解的方程问题。
四、 利用矩阵函数,线性代数思路解决问题
鸡兔问题是二元一次方程组,可以利用线性代数方法进行求解。根据题意列出二元一次方程组为: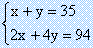
其中x为鸡数,y为兔数。根据方程组由线性代数方法可以列出如下两组矩阵A和矩阵B:
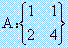
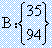
设所求矩阵为x,则方程组转化为AX=B,即 。
。
根据如上的数学分析,我们可以利用Excel中矩阵函数的独特功能,使用矩阵逆函数MINVERSE对矩阵A求逆,然后利用矩阵乘函数MMULT对矩阵A的逆矩阵和B矩阵进行乘法运算,得到的结果矩阵就是方程组的解。
具体做法如下(参见图 8):
1. 在A1:B2区域中输入矩阵A的数值,在D1:D2区域中输入矩阵B的数值;
2. 求取A的逆矩阵。选中B4:C5单元格,输入数组公式=MINVERSE(A1:B2),确认时必须按下Ctrl+Shift+Enter组合键;
3. 求取A的逆矩阵和B矩阵的乘积。选中B7:B8单元格,输入数组公式=MMULT(B4:C5,D1:D2),确认时必须按下Ctrl+Shift+Enter组合键;
4. B7、B8单元格的计算结果为23和12,即鸡数为23,兔数为12。
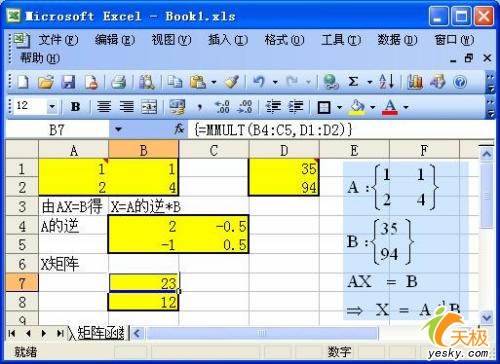
图 8 矩阵函数求解
使用矩阵函数的方法,在本质上是解决数学中的n元一次方程组的问题,具有比较广泛的通用性。
五、 使用VBA编程求解
鸡兔问题也可以编程解决。打开菜单“工具”à“宏”à“Visual Basic编辑器”,选择VBA编辑器的“插入”à“模块”菜单,并输入如下代码:
Sub chickrabbit()
For chick = 1 To 35
For rabbit = 1 To 35
If (chick + rabbit = 35) And (2 * chick + 4 * rabbit = 94) Then
MsgBox "鸡的数量为" & chick & ",兔为" & rabbit
End If
Next rabbit
Next chick
End Sub
编辑完毕后关闭VBA窗口,然后选择“工具”à“宏”,然后执行chickrabbit宏,就会弹出正确答案,如图 9所示。该程序可以做进一步的改进,例如可以改进执行方式、直接调用工作表数据、将输出结果显示在Excel单元格中等等,篇幅所限,不再赘述。

图9
本文分别使用了IF函数试探、双变量模拟运算表、规划求解、矩阵函数和VBA编程等方法对古典鸡兔问题进行求解,目的并不是求解简单数学问题的答案,而是旨在通过多种方法求解,展示Excel的多功能性和解决方式的灵活性,进一步开拓分析问题、解决问题的思路。